1、矿井瞬变电磁法
瞬变电磁的原理最早在1933年就被L.W.Blau提出,但由于采用脉冲激发,使得瞬变响应太低,分辨率不高[1]。20世纪中叶至七八十年代,国内外学者相继完善了地面瞬变电磁法的基础理论[2][3],瞬变电磁法开始进入实用阶段。进入21世纪以来,于景邨[4]、岳建华[5]等将瞬变电磁法应用于矿井中,地下全空间瞬变电磁得到较快发展。
矿井瞬变电磁法(Mine Transient Electromagnetic Method,简称MTEM)具有穿透高阻能力强、对低阻体反应灵敏的优点,受限于有限的巷道空间,矿井瞬变电磁法不可能像地面瞬变电磁那样采用大回线探测装置,只能采用边长小于3m的多匝小回线进行探测[4],相比于地面瞬变电磁法体积效应更小、横向分辨率更高。
矿井瞬变电磁法与其他地球物理方法一样,反演解释对整个勘探工作至关重要。受巷道空间限制,矿井瞬变电磁法只能采用小尺寸线框作为收-发装置,同时考虑到安全问题和浅部盲区范围,发射电流不宜过大(小于5A),激发能量减小导致信号减弱;另外,巷道中存在锚杆、铁轨、掘进机等金属干扰体,降低了资料的信噪比;加上电磁场在巷道及围岩中的传播存在全空间效应,信号包含了线圈法线两个方向的异常响应,这些问题给反演解释带来了困难[5][6]。
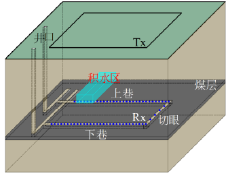
图1 井下瞬变电磁装置示意图 (引自文献[6])
2、钻孔瞬变电磁
钻孔瞬变电磁法,与常规的地-井和巷-井瞬变电磁法不同,它是将发射线圈和接收线圈置于钻孔中且始终同时移动逐点探测的一种探测方法。由于其特殊的探测环境,钻孔瞬变电磁方法探测装置与矿井瞬变电磁法有所不同,分为共轴探测和共面探测,共轴探测转置是发射线圈和接收线圈的法线位于同一直线上,共面探测装置是发射线圈和接收线圈位于同一个平面。
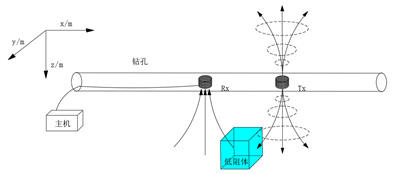
图2 钻孔瞬变电磁法探测原理示意图
目前针对矿井瞬变电磁数据的反演数据处理,主要以一维反演为主,包括阻尼最小二乘等局部最优化方法和粒子群算法等全局最优化方法,这类算法的特点是通过不断迭代的过程修改模型参数以实现目标函数最小化。其过程可分为三步:①根据实测数据或正演模型得到理论场值,作为观测数据;②以迭代初始模型进行正演计算得到场分量的正演响应值;③计算理论场值和正演场值的拟合误差,判断误差是否满足精度要求,若满足则停止迭代,输出模型参数;否则按照一定规则修改参数重新正演计算,直到满足拟合精度要求或达到迭代次数阈值。各种方法的优化过程类似,不同之处在于修改参数的机制以及反演迭代准则存在差别。
为了提升井下瞬变电磁数据的处理精度,国内学者开展了2.5维反演和基于人工智能方法的反演研究,为井下瞬变电磁勘探的精细化处理提供了新的研究方向。
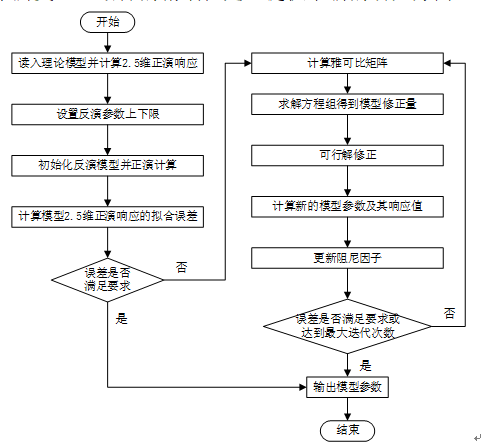
图3 2.5维瞬变电磁法反演流程图 (引自文献 [8])
21世纪以来,随着神经网络理论的完善和发展,诸多研究学者将神经网络算法引入到地球物理领域,尤其在地球物理勘探资料处理解释中,神经网络以其独特的非线性拟合能力在地球物理勘探中得到了广泛应用[10][11][12]。

图4 基于LSTM神经网络的反演算法整体框架(引自文献 [9])
3、模型测试
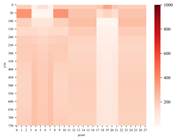
图5a为模型一示意图,图5b为OCCAM反演结果,图5c为神经网络反演结果,可以看出图5c中,煤层、断层和4个异常体的边界反映均较为清晰,尤其是埋深、厚度、上下界面都与设置值基本吻合,仅煤层厚度存在一定误差,而较宽的两个异常体,中间和两侧的厚度及上下边界也有一定误差,此外,除低阻异常体外的其他区域,电阻率值较设置值均偏低,但总体来看,反演精度显著高于OCAMM反演结果,与预设模型吻合度较高[9]。

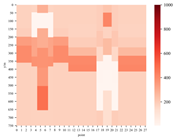
a b c
图5 模型示意图和反演结果 (引自文献 [9])
(a) 模型示意图 (b) OCAMM反演结果 (c) Seq2seq模型反演结果
图6a为模型二示意图,图6b为一维模拟退火粒子群算法反演结果,图6c为阻尼最小二乘2.5维反演结果,可以看出,相比于一维反演结果,图中地层边界更为明显,但反演剖面上假异常现象更加突出。
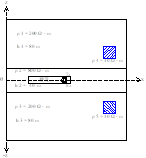
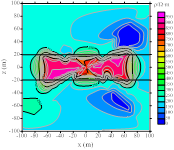
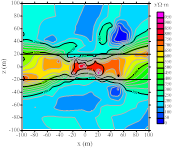
a b c
图5 模型示意图和反演结果 (引自文献 [8])
(b) 模型示意图 (b) 模拟退火粒子群算法一维反演结果 (c) 阻尼最小二乘法2.5维反演结果
[1] 李貅.瞬变电磁测深的理论与应用[M].西安:陕西科学技术出版社,2002.
[2] Kumar R, Das U C. Transformation of dipole to Schlunberger sounding curves by means of digital linear filters[J]. Geophysical Prospecting,1977,25:780-789.
[3] Markku P, Saurabh K V, Sven-Erik H. Inversion of transient electromagnetic profile data using conductive finite plate model Journal of applied[J]. Geophysics, 1998, 38:181-194.
[4] 于景邨,刘志新,刘树才, 等.深部采场突水构造矿井瞬变电磁法探查理论及应用[J].煤炭学报,2007(08):818-821.
[5] 岳建华, 杨海燕, 胡搏. 矿井瞬变电磁法三维时域有限差分数值模拟[J].地球物理学进展,2007(06):1904-1909.
[6] 李毛飞. 地面和地巷瞬变电磁法联合反演解释研究[D].中国矿业大学,2021.
[7] 王慧杰. 基于全卷积神经网络的钻孔瞬变电磁法预测岩层富水性研究演[D].中国矿业大学(北京),2022..
[8] 周金. 矿井瞬变电磁超前探测2.5维正反演[D].中国矿业大学(北京),2018..
[9] 范涛,薛国强,李萍,燕斌,鲍亮,宋金秋,任笑,李泽林.瞬变电磁长短时记忆网络深度学习实时反演方法[J].地球物理学 报,2022,65(09):3650-3663.
[10] 刘国辉,侯征,王天意,等. 一种新型的地下含水层涌水量预测模型[J].地球物理学进展, 2012, 27(03):1268-1273.
[11] 肖智兴,黄涛,李政,等. 遗传—神经网络算法在水下隧道涌水量预测中的应用[J].水资源与水工程学报, 2011, 22(03):102- 105.
[12] 王佩璐. 预测矿井涌水量的时间序列和BP神经网络耦合模型研究[D]. 焦作:河南理工大学, 2012.